netze/networks neural oscillators

Neural oscillators are interesting because they allow to create rhythmic behavior in a very elegant way. They can be realized with just two mathematical equations that describe the behavior of two mutually coupled systems in time. There are three implementations available for download, a pure data patch (puredata.info), an arduino sketch (arduino.cc) and a processing sketch (processing.org). The processing sketch is also used on this page to display the rhythmic behavior of two coupled neurons.

To understand the different parameters, the best is to play around with the pure data implementation, because you can modify all parameters of the two systems online and see their effect on the oscillation.

If you want something more physical you can use the arduino code and use the output of the excitatory neuron to rhythmically drive physical components such as a motor or a led. The arduino code is also best suited to understand how to program such dynamical systems.

background

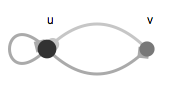
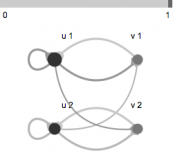
The first system is a self excitatory neuron that has a positive feedback connection onto itself, so when it becomes active it activates itself even more.

The second system is an inhibitory neuron that is activated by a positive connection from the excitatory neuron and it sends back negative (inhibitory) feedback to the self excitatory neuron. When the excitatory system becomes active it activates the inhibitory neuron, that in turn suppresses the activation of the excitatory neuron. Once the excitatory neuron is de-activated the inhibitory neuron looses the positive input and becomes inactive. Now without the inhibitory input the excitatory neuron becomes active and activates the inhibitory neuron again. A new cycle begins.

The mathematical equations for the neural oscillators presented here have first been fully analyzed by Shun-Ichi Amari (Amari 1977). Studies of this type of interaction within neural systems date back to work from cybernetic pioneers Norbert Wiener and Arturo Rosenblueth (Wiener and Rosenblueth 1946). The mathematical formalism to describe systems that evolve in time is the dynamical systems approach. A dynamical system describes the temporal evolution of a state variable in time. In case of the neural oscillators there are two state variables \(u\) and \(v\) that represent the neural activation level of the excitatory and of the inhibitory neuron. The temporal evolution of the state variable is described by making the state variable’s rate of change \(\dot{u}\) a function of it’s own state \(\dot{u}=f(u)\). For the neural oscillator the two equations describing the rate of change of the two neurons are as follows.

$$\tau\dot{u} = -u+h_u+c_{uu} \sigma(u) + c_{vu} \sigma(v) \\ \tau \dot{v} = -v+h_v+ c_{uv} \sigma(v)$$
Here \(\sigma(u)\) is a non-linear sigmoid function that is \(1\) for large values of \(u\) and \(0\) for values smaller than \(0\). The rate of change of the excitatory neuron \(\dot{u}\) depends on three parameters: the resting level \(h_u\), the self-interatcion \(c_{uu}\sigma(u)\) and the inhibition from \(c_{vu}\sigma(v)\). The equation for the rate of change of the inhibitory neuron \(\dot{v}\) has one parameter less, there is no self-interaction just input from the excitatory neuron \(c_{uv}\sigma(u)\) and the resting level \(h_v\).

literature references

Amari, S. (1977). Dynamics of pattern formation in lateral-inhibition type neural fields. Biological Cybernetics, 27:77–87 (link)
Wiener, N. and Rosenblueth, A. (1946). The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Archivos del instituto de Cardiologıa de Mexico, 16(3):205.